Regions of existence and uniqueness for singular two-point boundary value problems
Abstract
A monotone iterative technique with lower and upper solutions is presented to identify the regions of existence for the solutions of singular two-point boundary value problems
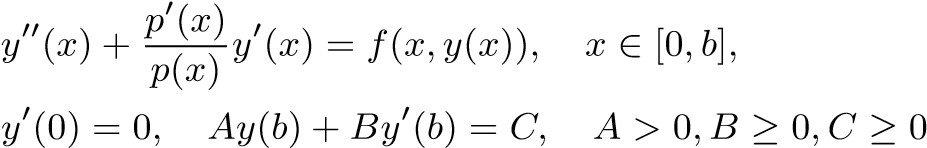
without requiring the monotonicity conditions on f(x,y). Under an additional condition on f(x,y), uniqueness of the solution is also established. These existence and uniqueness results are constructive and complement the existing results. Four examples including some engineering problems are given to illustrate the applicability of the proposed approach.
Keyword : singular boundary value problem, method of lower and upper solutions, existence and uniqueness, monotone iterative technique

This work is licensed under a Creative Commons Attribution 4.0 International License.
References
R.P. Agarwal and D. O’Regan. Singular initial and boundary value problems with sign changing nonlinearities. IMA Journal of Applied Mathematics, 65(2):173– 198, 2000. https://doi.org/10.1093/imamat/65.2.173
R.P. Agarwal and D. O’Regan. Some new results for singular problems with sign changing nonlinearities. Journal of Computational and Applied Mathematics, 113(1-2):1–15, 2000. https://doi.org/10.1016/S0377-0427(99)00239-3
R.P. Agarwal and D. O’Regan. CHAPTER 1 - A survey of recent results for initial and boundary value problems singular in the dependent variable. In A. Cañada, P. Drábek and A. Fonda (Eds.), Handbook of Differential Equations, volume 1 of Ordinary Differential Equations, pp. 1–68, Amsterdam, 2004. Elsevier. https://doi.org/10.1016/S1874-5725(00)80003-6
J.V. Baxley. Some singular nonlinear boundary value problems. SIAM Journal on Mathematical Analysis, 22(2):463–479, 1991. https://doi.org/10.1137/0522030
J.V. Baxley and G.S. Gersdorff. Singular reaction-diffusion boundary value problems. Journal of Differential Equations, 115(2):441–457, 1995. https://doi.org/10.1006/jdeq.1995.1022
M.M. Chawla and P.N. Shivakumar. On the existence of solutions of a class of singular nonlinear two-point boundary value problems. Journal of Computational and Applied Mathematics, 19(3):379–388, 1987. https://doi.org/10.1016/0377-0427(87)90206-8
C. De Coster and P. Habets. Two-Point Boundary Value Problems: Lower and Upper Solutions, volume 205 of Mathematics in Science and Engineering. Elsevier, Amsterdam, 2006.
A. Dinmohammadi, A. Razani and E. Shivanian. Analytical solution to the nonlinear singular boundary value problems arising in biology. Boundary Value Problems, 2017(1):63, 2017. https://doi.org/10.1186/s13661-017-0795-8
A. Dinmohammadi, E. Shivanian and A. Razani. Existence and uniqueness of solutions for a class of singular nonlinear two-point boundary value problems with sign-changing nonlinear terms. Numerical Functional Analysis and Optimization, 38(3):344–359, 2017. https://doi.org/10.1080/01630563.2016.1276073
D.R. Dunninger and J.C. Kurtz. Existence of solutions for some singular boundary value problems. Journal of Mathematical Analysis and Applications, 115(2):396–405, 1986. https://doi.org/10.1016/0022-247X(86)90003-X
A.M. Fink, J.A. Gatica, G.E. Hernandez and P. Waltman. Approximation of solutions of singular second-order boundary value problems. SIAM Journal on Mathematical Analysis, 22(2):440–462, 1991. https://doi.org/10.1137/0522029
W.F. Ford and J.A. Pennline. Singular non-linear two-point boundary value problems: Existence and uniqueness. Nonlinear Analysis: Theory, Methods & Applications, 71(3):1059–1072, 2009. https://doi.org/10.1016/j.na.2008.11.045
J.A. Gatica, G.E. Hernandez and P. Waltman. Radially symmetric solutions of a class of singular elliptic equations. Proceedings of the Edinburgh Mathematical Society, 33(2):169–180, 1990. https://doi.org/10.1017/S0013091500018101
J.A. Gatica, V. Oliker and P. Waltman. Singular nonlinear boundary value problems for second-order ordinary differential equations. Journal of Differential Equations, 79(1):62–78, 1989. https://doi.org/10.1016/0022-0396(89)90113-7
R. Kannan and D. O’Regan. Singular and nonsingular boundary value problems with sign changing nonlinearities. Journal of Inequalities and Applications, 5(6):621–637, 2000.
H.B. Keller. Numerical Methods for Two-Point Boundary-Value Problems. Blaisdell Publishing Co., Waltham, MA, 1968.
W.G. Kelly and A.C. Peterson. The Theory of Differential Equations: Classical and Qualitative. Springer, New York, 2010. https://doi.org/10.1007/978-1-4419-5783-2
G.S. Ladde, V. Lakshmikantham and A.S. Vatsala. Monotone Iterative Techniques for Nonlinear Differential Equations. Pitman, Boston, MA., 1985.
H. Lü and Z. Bai. Positive radial solutions of a singular elliptic equation with sign changing nonlinearities. Applied Mathematics Letters, 19(6):555–567, 2006. https://doi.org/10.1016/j.aml.2005.08.002
J.J. Nieto. An abstract monotone iterative technique. Nonlinear Analysis: Theory, Methods & Applications, 28(12):1923–1933, 1997. https://doi.org/10.1016/S0362-546X(97)89710-6
D. O’Regan. Theory of Singular Boundary Value Problems. World Scientific, Singapore, 1994. https://doi.org/10.1142/2352
D. O’Regan. Existence theory for nonresonant singular boundary value problems. Proceedings of the Edinburgh Mathematical Society, 38(3):431–437, 1995. https://doi.org/10.1017/S0013091500019246
D. O’Regan. Upper and lower solutions for problems with singular sign changing nonlinearities and with nonlinear boundary data. Topological Methods in Nonlinear Analysis, 19(2):375–390, 2002.
D. O’Regan and R.P. Agarwal. Singular problems: An upper and lower solution approach. Journal of Mathematical Analysis and Applications, 251(1):230–250, 2000. https://doi.org/10.1006/jmaa.2000.7043
R.K. Pandey. On a class of regular singular two point boundary value problems. Journal of Mathematical Analysis and Applications, 208(2):388–403, 1997. https://doi.org/10.1006/jmaa.1997.5320
R.K. Pandey and A.K. Verma. Existence-uniqueness results for a class of singular boundary value problems arising in physiology. Nonlinear Analysis: Real World Applications, 9(1):40–52, 2008. https://doi.org/10.1016/j.nonrwa.2006.09.001
R.K. Pandey and A.K. Verma. A note on existence-uniqueness results for a class of doubly singular boundary value problems. Nonlinear Analysis: Theory, Methods & Applications, 71(7-8):3477–3487, 2009. https://doi.org/10.1016/j.na.2009.02.012
J. Pennline. Constructive existence and uniqueness for some nonlinear two-point boundary value problems. Journal of Mathematical Analysis and Applications, 96(2):584–598, 1983. https://doi.org/10.1016/0022-247X(83)90062-8
I. Rachůnková, O. Koch, G. Pulverer and E. Weinmüller. On a singular boundary value problems arising in the theory of shallow membrane caps. Journal of Mathematical Analysis and Applications, 332(1):523–541, 2007. https://doi.org/10.1016/j.jmaa.2006.10.006
R.D. Russell and L.F. Shampine. Numerical methods for singular boundary value problems. SIAM Journal on Numerical Analysis, 12(1):13–36, 1975. https://doi.org/10.1137/0712002
E. Shivanian. Existence and uniqueness analysis for a class of singular non-linear two-point boundary value problems by an optimal iterative sequence. International Journal of Industrial Mathematics, 15:1–10, 2023. https://doi.org/10.30495/IJIM.2022.44028.1312
A.K. Verma, B. Pandit, L. Verma and R.P. Agarwal. A review on a class of second order nonlinear singular BVPs. Mathematics, 8(7):1045, 2020. https://doi.org/10.3390/math8071045
A.K. Verma, M. Singh and R.P. Agarwal. Regions of existence for a class of nonlinear diffusion type problems. Applicable Analysis and Discrete Mathematics, 14(1):106–121, 2020. https://doi.org/10.2298/AADM190219013V
